Bulk Volume Classification 批量成交量分类算法

作者：MR. HUA　发表时间：2024-10-28　阅读次数：82

随着⾼频交易的兴起，传统的交易分类算法变得越来越难以应对复杂的市场环境。交易者的买卖意图隐藏在⼤量碎⽚化的订单中，⽽诸如撤单、隐藏订单等交易⾏为更增加了交易数据解读的难度。本⽂将介绍⼀种创新的交易分类算法 —— Bulk Volume Classification (BVC)，并探讨它与其他算法的优缺点。
⼀、交易分类算法
（一）Tick Rule 涨跌规则算法 – 传统的交易分类算法
1. 若当前交易的价格大于前一笔交易的价格，则将其归类为买入。
2. 若当前交易的价格小于前一笔交易的价格，则将其归类为卖出。
3. 若当前交易的价格等于前一笔交易的价格，则将其归类为上一个bar的分类。
（二）Aggregate Tick Rule 聚合涨跌规则算法 - Tick Rule的衍生
在以一段时间或一定成交量为基准的bar中，Tick Rule分类为买入的样本量之和为买入量、Tick Rule分类为卖出的样本量之和为卖出量，我们将之称为Aggregate Tick Rule。
（三）Bulk Volume Classification 批量成交量分类算法
在以一段时间或一定成交量为基准的bar中，利⽤bar中的价格变动和价格变动标准差来推断买卖单的⽐例并算出买入量和卖出量。
BVC算法的公式：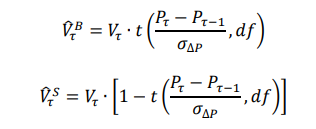

BVC公式说明：

1730097284744

二、分类算法之间比较的方法论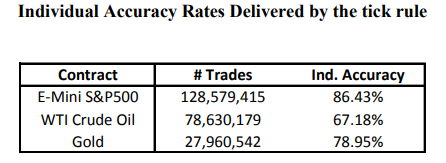
通过三个维度来验证不同分类算法的正确性，分别是：
1. 计算分类算法基于价格对买卖的判断和实际的主动买卖标记（aggressor flags）做对比并计算算法的正确性。
2. 用不同算法计算订单流不平衡值（order flow imbalance），并将其与价差作回归分析。从逻辑上来看若交易包含了有效信息，订单流不平衡值和价差应该成正相关。
3. 计算日度的订单流不平衡值和日度价格变动作回归分析，因为短期的订单流不平衡值若反映了有效信息，做市商的做市意愿会被影响，从而影响了市场的有效性，而长期来看市场的有效性会影响市场的价格。
三、分类算法的比较结果
1. 分类算法基于价格对买卖的判断和实际的主动买卖标记做对比：
验证标的为E-mini S&P 500期货（CME）、WTI原油期货（NYMEX）、黄⾦期货（COMEX），数据时间为2010年11月至2011年11月。
Tick Rule 逐笔的正确性

Aggregate Tick Rule 和 BVC在不同的秒级时间bar和交易量bar的正确性对比：
（1）E-mini S&P 500期货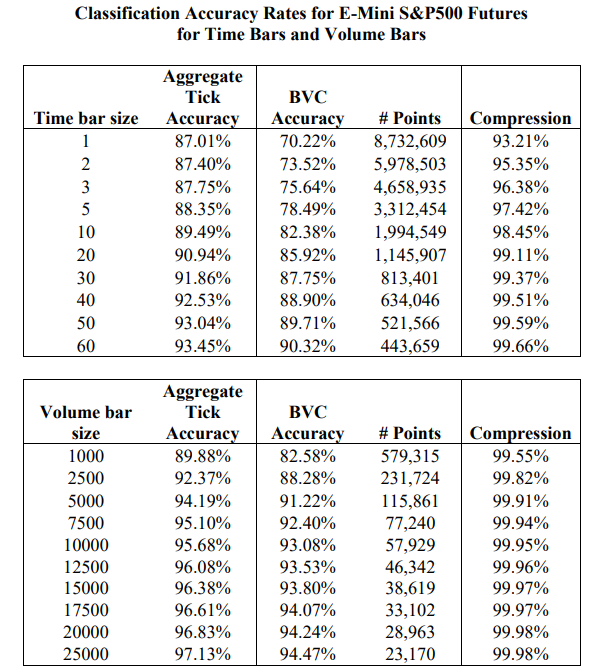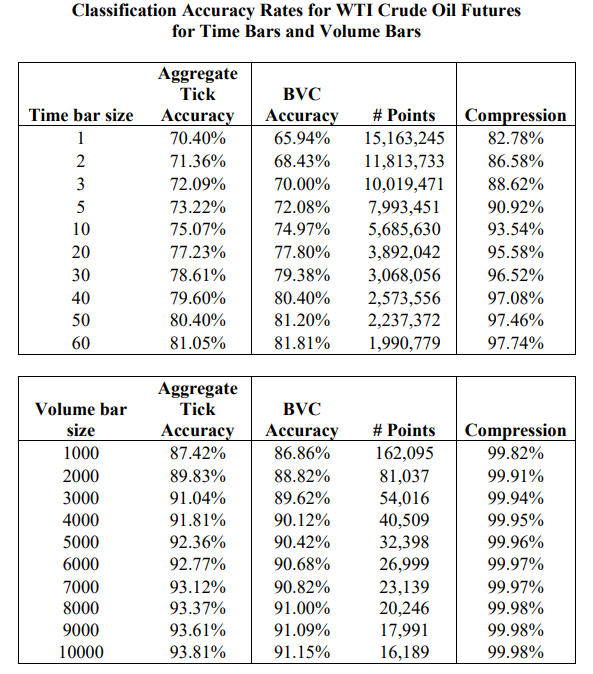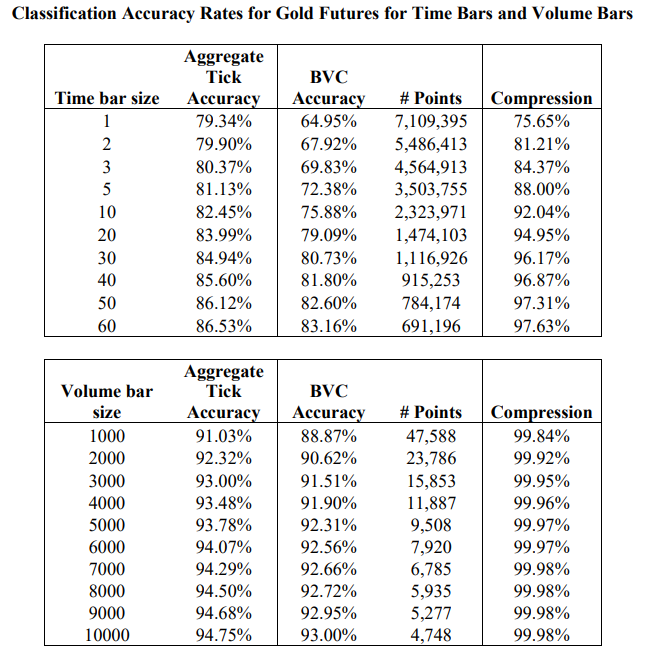

（2）WTI原油期货

（3）黄⾦期货

从以上实验结果我们可以看出，聚合Tick Rule算法整体比逐笔的Tick Rule正确性高，因为逐笔的Tick Rule显而易见包含了更多的噪音；同样当时间bar较长时BVC算法的正确性也比逐笔的Tick Rule算法的正确性高；在以交易量为基准作的bar中，BVC算法的正确性往往也占据了上风；在对比聚合Tick Rule算法和BVC算法时我们发现，在e-mini期货和黄金期货中，聚合Tick Rule算法的正确性更高，但是在交易更活跃噪音也更多的WTI原油期货中，时间bar的BVC算法正确性更高。
2. 回归分析订单流不平衡值和价差的关系
计算订单流不平衡值（OI, order imbalance）的公式为：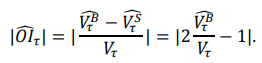

即订单流不平衡值 = |（买入量-卖出量）/（成交量）|
将聚合Tick Rule的OI值和BVC算法的OI值分别、同时作为自变量，价差（spread）作为因变量，作回归分析，标的为E-mini S&P 500期货，结果如下：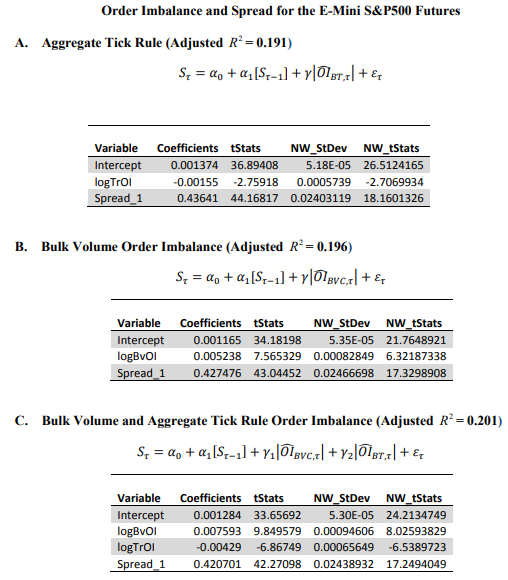

如上文所说，若交易包含了有效信息，订单流不平衡值和价差应该成正相关，即订单流不平衡值越大，价差越大。聚合Tick Rule算法计算的OI值的系数是负数，即订单流差越小，价差越大。相比之下BVC算法计算的OI的系数是正的且更显著。若将两个算法计算的OI同时作为因变量作回归分析，从回归结果来看我们可以得到同样的结论，即BVC算法的OI值可以检测到交易反映的有效信息，但是聚合Tick Rule算法的OI值不可以。
3. 计算日度的订单流差指标和日度价格变动作回归分析
实验标的同样为2010年11月至2011年11月的E-mini S&P 500期货，该标的在该时间区间内日均成交量≈329000，所以此实验将按成交量捏bar，每个bar有10000手，每天共有30个bar，日度OI值为每天30个bar的OI值的平均值，日度价格变动为每天第一个bar到第三十个bar的价格变动。
回归结果：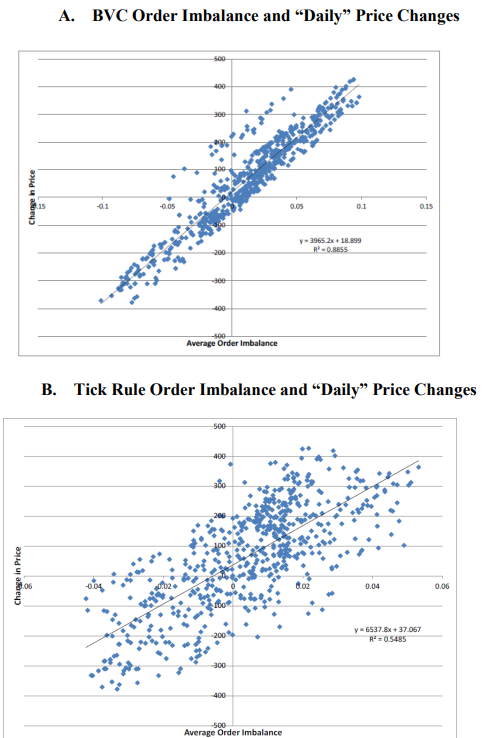

可见BVC算法的OI值和价格变动的相关性更大，且BVC算法的OI值作为自变量的R-squared为0.89，而Tick Rule算法的OI值作为自变量的R-squared仅为0.55。所以在这个维度，BVC算法更为有效。
四、分类算法之间比较的结论
- Tick Rule算法：简单且快速，但在噪声⼤的市场中易受⼲扰，且需要逐笔数据。
- 聚合Tick Rule算法：在⼀定程度上减少了误差，噪音少时效果强于BVC，但在⾯对复杂市场环境时精度不及BVC，同样需要逐笔数据。
- BVC算法：噪声处理能⼒强、减少分类偏差且能⼤幅提⾼数据压缩效率（因为不需要逐笔数据），同时包含更多的潜在有效信息，对日度价格变动也有更强的解释性。
五、BVC的应⽤场景和展望
BVC算法适⽤于⾼频交易，结合高频模型来预测短期价格变动。同时从上文的BVC算法的OI值和日度价格变动的回归分析可见，BVC算法的日度值也可以作为一个中低频的截面因子在多空策略中使用，国内的一些报告探究了BVC因子在A股市场的效果，参数优化后的夏普在1.5左右。未来，BVC算法有望与机器学习和订单簿分析等⼯具结合，为市场研究和交易策略提供更深⼊的洞察。

参考文献：
[1] Easley, D. , Prado, M. M. L. D. , & O'Hara, M. (2013). Bulk classification of trading activity. SSRN Electronic Journal.
[2] Chakrabarty, B. , Pascual, R. , & Shkilko, A. . (2015). Evaluating trade classification algorithms: bulk volume classification versus the tick rule and the lee-ready algorithm. Journal of Financial Markets, 25(sep.), 52-79.