| 量化中的数据降噪 |
| 作者:Mr.FENG 发表时间:2024-03-27 阅读次数:1899 |
在量化交易领域,数据的质量和准确性对于构建稳健的交易策略至关重要。然而,市场数据往往受到各种噪音和干扰的影响,这些噪音可能来自于数据收集过程中的误差、交易所的错误报价或者市场上的突发事件。因此,为了准确地分析市场并制定有效的交易决策,量化交易者需要采取一系列的数据降噪方式来清理和处理原始数据。本文将详细的介绍一些常见的数据降噪方式。
一、移动平均 1.1简单移动平均(SMA)简单移动平均是最基本的移动平均方法之一,它的计算方式非常简单,即对一定时间段内的数据值取平均。例如,若我们希望计算五天的简单移动平均,只需将过去五天的收盘价加总,然后除以五即可得到五日简单移动平均值。随着新的数据点的加入,旧数据点则从计算中被移除。 1.2指数加权移动平均(EMA) 指数加权移动平均是另一种常见的移动平均方法,与简单移动平均相比,它赋予了最近的数据点更大的权重。这意味着指数加权移动平均对于最近的数据点更为敏感,能够更快地反映出市场的变化。指数加权移动平均的计算公式如下: EMAt=α⋅Pricet+(1−α)⋅EMAt−1 其中,EMAt是当前时刻的指数加权移动平均值,Pricet是当前时刻的价格,α是平滑系数,通常取值在0到1之间。较小的 α会使得指数加权移动平均对最新数据点的反应更加迅速,但也会增加噪音的敏感度。
1.3移动平均的应用 移动平均常用于量化交易策略中的信号生成和趋势跟踪。例如,当短期移动平均线(如5日或10日移动平均线)穿越长期移动平均线(如50日或200日移动平均线)时,可能会产生买入或卖出信号。此外,移动平均也可用于构建技术指标,如MACD(移动平均收敛/发散)和Bollinger Bands(布林带)等,用于辅助交易决策。综上所述,移动平均是一种简单而有效的数据降噪方法,可用于消除市场数据中的噪音并揭示出长期趋势,从而辅助量化交易者制定有效的交易策略。
二、滤波器 滤波器是一种常用的数据降噪技术,在信号处理、时间序列分析以及图像处理等领域广泛应用。它通过改变信号的频率特性,抑制或增强特定频率的成分,从而实现对信号的去噪或特征提取。在量化交易中,滤波器可以用来去除市场数据中的噪音,揭示出数据的潜在趋势和周期性,从而帮助量化交易者制定更为准确的交易策略。 2.1线性滤波器 线性滤波器是一种常见的滤波器类型,它基于线性加权对输入信号进行处理。常见的线性滤波器包括: 低通滤波器(Low-pass Filter):低通滤波器允许低频信号通过,同时抑制高频信号。在量化交易中,低通滤波器可以用来平滑价格数据,去除高频波动,揭示出长期趋势。 高通滤波器(High-pass Filter):高通滤波器允许高频信号通过,同时抑制低频信号。它可以用于去除价格数据中的低频噪音,突出价格的短期波动。 带通滤波器(Band-pass Filter):带通滤波器可以选择性地通过一定范围内的频率成分,同时抑制其他频率成分。在量化交易中,带通滤波器可用于识别特定周期的周期性信号。 带阻滤波器(Band-stop Filter):带阻滤波器可以选择性地抑制一定范围内的频率成分,同时允许其他频率成分通过。它常用于去除特定频率范围内的噪音。
2.2非线性滤波器 非线性滤波器不遵循线性加权的原理,它通过非线性运算对信号进行处理。常见的非线性滤波器包括:中值滤波器(Median Filter):中值滤波器将每个像素的值替换为其周围像素值的中值。它能够有效地去除椒盐噪声等局部噪音。 自适应滤波器(Adaptive Filter):自适应滤波器根据输入信号的特性自动调整滤波器的参数。它可以适应信号的变化,并根据需要调整滤波效果。
2.3滤波器的运用 滤波器在量化交易中的应用非常广泛。例如,可以使用低通滤波器平滑价格数据,去除噪音和短期波动,从而揭示出长期趋势;可以使用带通滤波器识别特定周期的周期性信号,如季节性效应;还可以使用中值滤波器去除椒盐噪声等局部噪音。综上所述,滤波器是一种常用的数据降噪技术,可以根据信号的特性选择合适的滤波器类型和参数,从而实现对市场数据的去噪和特征提取,为量化交易提供更准确的分析和预测。
三、小波变换 小波变换(Wavelet Transform)是一种信号处理技术,用于分析信号的频率特征和时域特征。与傅里叶变换相比,小波变换更适用于分析非平稳信号,因为它能够在不同时间尺度上对信号进行分析,从而揭示出信号的局部特征和变化。在量化交易领域,小波变换被广泛应用于时间序列数据的分析和预测,可用于去除市场数据中的噪音、检测周期性成分以及提取信号的特征。
3.1连续小波变换 连续小波变换将信号与一组小波基函数进行卷积,以在不同的尺度和位置上分析信号。小波基函数是由一个母小波函数和尺度参数组成,它可以被平移和缩放以适应不同的信号特征。连续小波变换的数学表示如下: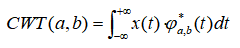 其中, 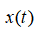 是输入信号, 尺度参数为a,平移参数为 b 的小波基函数, 是输入信号, 尺度参数为a,平移参数为 b 的小波基函数,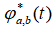 是其复共轭。连续小波变换产生的系数可以提供信号在不同尺度和位置上的频率信息,被用来分析信号的时频特征。 是其复共轭。连续小波变换产生的系数可以提供信号在不同尺度和位置上的频率信息,被用来分析信号的时频特征。
3.2离散小波变换 离散小波变换是连续小波变换的离散形式,通过将信号分解成不同尺度上的近似系数和细节系数来分析信号。离散小波变换通常通过多层级的分解来实现,每一级分解都将信号分解为近似系数和细节系数。近似系数表示信号的低频成分,细节系数表示信号的高频成分。通过多级分解,可以将信号的频率特征分解到不同的尺度上。离散小波变换可以用来去除信号中的噪音、压缩信号以及检测信号的突变点等。
3.3小波包变换 小波包变换是离散小波变换的扩展,它将信号进行更为详细的分解,以提供更丰富的频率信息。小波包变换在每一级分解时都对信号进行二分,将信号分解为更多的子频带。这样可以更精细地分析信号的频率特征,从而更准确地揭示信号的特征和结构。
3.4运用 在量化交易中,小波变换可以用于多个方面,包括:去噪:小波变换可以将信号分解为不同尺度上的成分,因此可以用于去除市场数据中的噪音,揭示出信号的真实结构和特征。 特征提取:小波变换可以提取信号的频率特征和时域特征,因此可以用于识别市场数据中的周期性成分、趋势以及突变点等。 压缩:小波变换可以通过丢弃低幅度的小波系数来实现信号的压缩,从而减小数据存储和传输的成本。 综上所述,小波变换是一种强大的信号处理技术,能够在不同尺度上对信号进行分析,揭示出信号的局部特征和频率特征。在量化交易中,小波变换可以用于去噪、特征提取以及信号压缩等方面,为量化交易提供更准确和有效的分析工具。 四、机器学习 在量化金融领域,数据的质量对于构建有效的量化模型至关重要。市场数据中常常存在各种噪音和异常值,这些噪音可能会干扰量化模型的建模和预测能力。因此,机器学习技术被广泛应用于量化金融中的数据降噪。
4.1基于模型的数据降噪 基于模型的数据降噪方法使用机器学习模型来识别和去除数据中的噪音。这些模型可以是监督学习模型、无监督学习模型或半监督学习模型。监督学习模型:例如,使用分类模型或回归模型来预测数据的目标值,然后将预测值与实际值进行比较,识别和去除异常值。 无监督学习模型:例如,使用聚类模型来识别数据中的簇,然后将异常簇识别为噪音并进行去除。 半监督学习模型:利用少量的标记数据和大量的未标记数据,结合监督学习和无监督学习的方法来进行数据降噪。
4.2基于深度学习的数据降噪 深度学习是机器学习领域的一种强大技术,在数据降噪方面也表现出了良好的效果。深度学习模型如自动编码器、生成对抗网络(GAN)等可以学习数据的复杂结构,并生成干净的数据。自动编码器:通过训练自动编码器来学习数据的表示,然后利用学习到的表示进行数据降噪。 生成对抗网络:使用生成对抗网络来学习数据的分布,并生成干净的数据样本,以用于数据降噪。 综上所述,机器学习在量化金融中的数据降噪方面有着广泛的应用,能够帮助量化交易者提高数据质量,并提高量化模型的预测准确性和稳健性。
4.3总结 机器学习在金融量化中的数据降噪方面有着广泛的应用,可以帮助提高数据的质量和准确性,从而提高量化模型的预测能力和稳健性。通过选择合适的机器学习模型和算法,量化分析人员可以更好地处理金融市场数据,并提高量化策略的有效性和可靠性。
五、总结 在金融量化中,数据降噪是非常重要的一步,它能够帮助提高量化模型的准确性和稳健性,从而提高投资决策的成功率和盈利能力。通过机器学习技术,我们可以对各种类型的金融数据进行有效的降噪处理,包括时间序列数据、图像数据和声音数据等。选择合适的数据降噪方法和机器学习模型,可以帮助量化分析人员更好地理解市场情况,更精准地进行量化建模和预测。因此,在进行量化分析和策略设计时,充分利用机器学习在数据降噪方面的能力将是非常有益的。通过不断优化和改进数据降噪方法,我们可以更好地利用金融市场数据,实现更稳定和可靠的量化交易策略。参考文献 [1]冉启文.小波变换与分数傅里叶变换理论及应用[M].哈尔滨工业大学出版社,2001. [2]李君卓.人工智能技术在金融数据处理领域的应用[J].中国科技期刊数据库 工业A, 2021. |
