遗传算法，是计算数学中用于解决最优化的搜索算法，是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等。

遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题，一定数量的候选解（称为个体）可抽象表示为染色体，使种群向更好的解进化。传统上，解用二进制表示（即0和1的串），但也可以用其他表示方法。进化从完全随机个体的种群开始，之后一代一代发生。在每一代中评价整个种群的适应度，从当前种群中随机地选择多个个体（基于它们的适应度），通过自然选择和突变产生新的生命种群，该种群在算法的下一次迭代中成为当前种群。

遗传算法中每一条染色体，对应着遗传算法的一个解决方案，一般我们用适应性函数（fitness function）来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。 可以这样想象，这个多维曲面里面有数不清的“山峰”，而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的，那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰，而不是陷落在一些小山峰。

首先寻找一种对问题潜在解进行“数字化”编码的方案。（建立表现型和基因型的映射关系）然后用随机数初始化一个种群（那么第一批爬山的袋鼠就被随意地分散在山脉上），种群里面的个体就是这些数字化的编码。接下来，通过适当的解码过程之后（得到袋鼠的位置坐标），用适应性函数对每一个基因个体作一次适应度评估（袋鼠爬得越高，越是受我们的喜爱，所以适应度相应越高）。用选择函数按照某种规定择优选择（我们要每隔一段时间，在山上射杀一些所在海拔较低的袋鼠，以保证袋鼠总体数目持平。）。让个体基因变异（让袋鼠随机地跳一跳）。然后产生子代（希望存活下来的袋鼠是多产的，并在那里生儿育女）。遗传算法并不保证你能获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。（你不必去指导袋鼠向那边跳，跳多远。）而只要简单的“否定”一些表现不好的个体就行了。（把那些总是爱走下坡路的袋鼠射杀，这就是遗传算法的精粹）

所以我们总结出遗传算法的一般步骤：

开始循环直至找到满意的解。

1.评估每条染色体所对应个体的适应度。

2.遵照适应度越高，选择概率越大的原则，从种群中选择两个个体作为父方和母方。

3.抽取父母双方的染色体，进行交叉，产生子代。

4.对子代的染色体进行变异。

5.重复2，3，4步骤，直到新种群的产生。

结束循环

 遗传算法的有趣应用很多，诸如寻路问题，8数码问题，囚犯困境，动作控制，找圆心问题（在一个不规则的多边形中，寻找一个包含在该多边形内的最大圆圈的圆心），TSP问题，生产调度问题，人工生命模拟等。下面以策略回测参数优化应用为例简单讲解

从应用的角度来讲，与遗传算法（或者其他任何智能优化算法）对应的，叫做穷举算法（又名暴力求解，Brute-force Search），我们以vn.py中的经典CTA策略(AtrRsiStrategy)为例简单讲解效果

• atr_length参数（默认22）：从10到40，步进1，总样本32
• atr_ma_length参数（默认10）：从4到20，步进2，总样本9
• rsi_length参数（默认5）：从3到20，步进1，总样本18

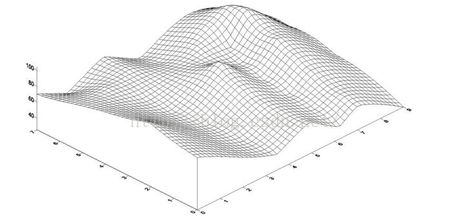
如果用穷举算法的话，我们一共执行 32 x 9 x 18 = 5184 次回测计算（三个参数所有样本的排列组合数量），即时在一台8核机器上也要跑648轮，相当长的一段时间了。

我们知道，随着策略的参数变化，最终的优化结果（又称目标函数，比如Sharpe Ratio）的变化并不是完全随机的，而是存在着一定的相关性，比如当atr_length处于18-25范围内的优化结果可能都比较好（先不考虑另外两个参数），如果到38上方可能就全都是亏钱的情况。

以布林带策略（BollStrategy）的参数优化为例：

• 使用的机器是一台阿里云的2核4G云服务器（CPU主频2.5G）
• 使用3年的股指连续合约的1分钟线数据，一共有三个参数参与优化，总样本空间韦13824个
• 多进程穷举算法的总优化时间为357分钟（双核跑满）
• 单进程遗传算法的总优化时间为27分钟（单核跑满）

由此可以看出，遗传算法相比穷举算法大大缩短了时间，提高了效率。

本文案例测试部分引用知乎vnpy专栏下博主【用python的交易员】的原创文章，原文链接：https://zhuanlan.zhihu.com/p/66403128